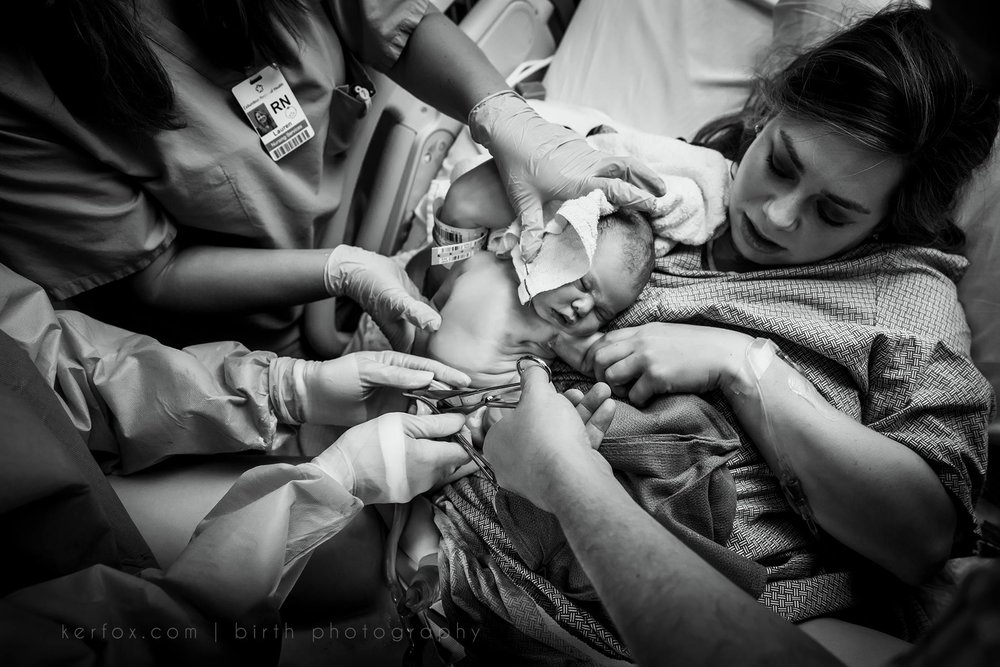
This girl right here. Well, she and her family hold a very special place in my heart. I was there to photograph Jim asking her to marry him, I also shot their engagement photos, their wedding, their maternity session, and now the birth of their precious Cora. Alex’s dad is also our pediatrician, and in my early days of motherhood helped me navigate some scary time with my Finley. He’s also been with us through countless cold and sick seasons with our other child that has zero immunity to anything.
Alex also helped babysit my kiddos a couple of years ago, she was one of the handful of people who would come to my rescue to watch my babies, when I would get calls from mom’s in labor. Watching her, and getting to know her, I knew motherhood would find her well when the time came. And I was right. She was made for this. She owned her labor, she’s thriving in motherhood, and I couldn’t be more proud of her.
And Jim, well, Jim steals the show guys. Alex did all the hard work but he supported her so beautifully, and so selflessly. Oh and his reaction to momma pushing and baby being born…. I’m warning you now, go grab some tissues. It’s the sweetest dad reaction to date!